Multithreaded matrix multiplication in Rust - Part II

Part I

This post is the second in a short series on writing efficient multithreaded matrix multiplication in Rust. The first post mentioned the divide and conquer algorithm and showed some benchmarks. In this post I’ll discuss the steps taken after and some more results.

This has proven to be an interesting, and as expected, difficult task! As I mentioned in the previous post my next steps were going to be to trim off some of the overhead. This was mostly a lot of unnecessary data copying. For each multiplication task I was creating a new Matrix struct and then concatenating these all together in the end. Thanks to matrixmultiply this isn’t necessary.

The new approach is to allocate all the memory for the output Matrix at the start and then populate this as we go. However this does have some caveats. Please excuse the poor quality of the diagram below. The algorithm is also described here.

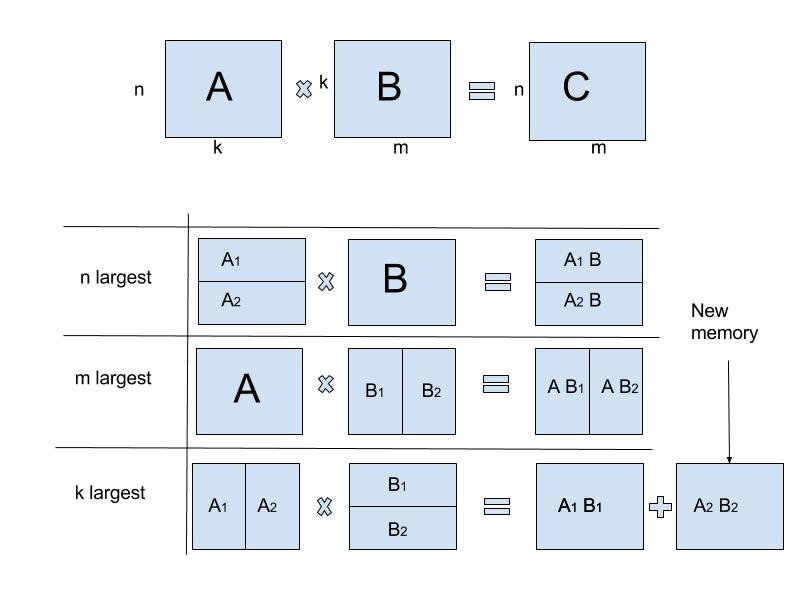
The first two rows from the image (n/m largest) are the simplest to implement. We split one of the input matrices in half and additionally split the output matrix in the same way. We then pass these respective components back into our multiplication function.

The third row is a little more complex. The output of each multiplication call will be the same size and then are added together. We cannot use the same output memory for each call - but we can create a new matrix for the output block and add this to our initial output matrix. This is detailed at the end of the third row. There is some complication here as the initial output matrix may not contain contiguous data. Vectorizing this sum is non-trivial but I won’t go into the details here.

The benchmarks

Conveniently I only focused on the k largest case in my last post - which actually worked pretty well. Here are the benchmarks for the n largest case.

test linalg::matrix::mat_mul_5000_20_20         ... bench:     462,425 ns/iter (+/- 25,718)
test linalg::matrix::mat_paramul_5000_20_20     ... bench:   1,159,495 ns/iter (+/- 408,637)

There’s no mistake there - the overhead copying cost completely dominated the multiplication. Now, with the new algorithm:

test linalg::matrix::mat_mul_5000_20_20         ... bench:     461,276 ns/iter (+/- 7,151)
test linalg::matrix::mat_paramul_5000_20_20     ... bench:     380,743 ns/iter (+/- 290,925)

We do much better on the n/m large case than before. However, the improvements for n/m are far less significant than for k large (which still provides an ~2x speedup). I haven’t quite figured out why…

What now?

There is still some work we can do along this path. Though most of the overhead has been removed we should still do some parameter tweaking. Currently we’re use the cpu count as the number of parallel threads - we could experiment with this. Some quick testing showed that 256 was a good threshold for dividing the matrix but we can explore this further. There are some other tweaks we should explore.

However, it is pretty likely that we’re nearing the cap of how successful this method can be. It is probably worth looking into multithreading the BLIS algorithm used by matrixmultiply.